Основы

Для того чтобы лучше понять суть табличного алгоритма вычисления CRC, обратимся опять к прямому методу, точнее к той схеме его вычисления (см. Рисунок 9.6), которая была реализована в приведенной выше программе.

Из этой схемы видно, что для текущего содержимого старшей половины регистра ЕАХ можно прогнозировать, как будет изменяться содержимое его битов по мере их сдвига. Для этого достаточно подвергнуть анализу его биты начиная с самого старшего. Допустим, что старшие 8 бит ЕАХ равны а7 а6 а5 а4 а3 а2 а, а,,. При следующем сдвиге (см. Рисунок 9.6) прямой алгоритм определяет, будет ли произведена операция XOR операнда с полиномом b7 b6 b5 b4 Ь3 b2 b, bо в ВХ (а7=1) или нет (а7=0). Если выдвинутый бит был равен 1, то прежнее содержимое старшей половины регистра ЕАХ будет подвергнуто операции XOR с соответствующими битами полинома. В обратном случае, если выдвинутый бит был равен 0, значения битов будут не изменены, а просто сдвинуты влево на одни разряд. В принципе, имея большое желание, можно рассчитать заранее, каким будет содержимое к-го бита в к-й итерации сдвига. К примеру, значение нового старшего бита, определяющего действия алгоритма в следующей итерации, можно рассчитать по содержимому двух старших битов старшего байта исходного операнда — а6 XOR а7 AND b7, где b7 — старший бит полинома (всегда равный единице).

Теперь остановимся для того, чтобы рассмотреть и обсудить очередную схему (Рисунок 9.7).

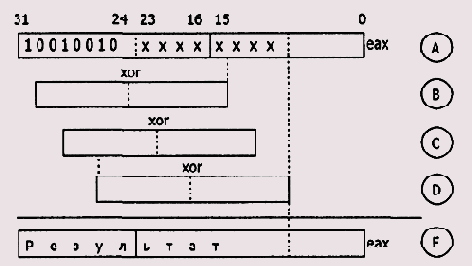
Рисунок 9.7. Влияние на регистр ЕАХ серии операций XOR при вычислении CRC

Из рассуждений выше следует, что если взять для рассмотрения старший байт операнда, то по его содержимому можно однозначно предположить, сколько операций XOR и когда будет выполнено (см. рисунок). Обозначим старшую половину регистра ЕАХ как переменную А, а операнды со значениями полинома, объединяемые с А при единичном состоянии очередного выдвигаемого слева бита, обозначим соответственно как В, С, D (помним, что В = С = D). Тогда формирование результата Е можно представить формулой:

Е-((А [сдвиги| XOR В) [сдвигиj XOR С) |сдвиги| XOR D

Здесь | сдвиги | представляют собой значение от 0 до 7 и определяются теку щим содержимым старшего байта операнда (регистра ЕАХ). Благодаря ассоциативному свойству операции XOR тот же самый результат можно получить, если предварительно выполнить операцию XOR над полиномами В, С, D с соответствующими значениями сдвигов, а затем результат объединить по XOR с А:

F: = 1 сдвиги| XOR ( В |сдвиги| XOR С |сдвиги| XOR D) Е:= A XOR F

Из этих рассуждений следуют важные выводы:

величина F является совершенно точно предсказуемой по содержимому старшего байта операнда;

если величина F определяется содержимым старшего байта операнда и собственно значением полинома, то существует всего 256 возможных значений этой величины (по количеству значений, представимых беззнаковым байтом);

исходя из первых двух положений величина F не зависит от значения операнда и может быть рассчитана заранее, при этом результаты ее расчетов можно свести в таблицу (!).

Вот мы и выяснили, на чем основано название табличного алгоритма расчета CRC. Теперь со знанием сути дела приведем его общее описание (Рисунок 9.8). В качестве основы для рассуждений по-прежнему используем программу прямого вычисления значения CRC и соответствующую схему (см. Рисунок 9.6).

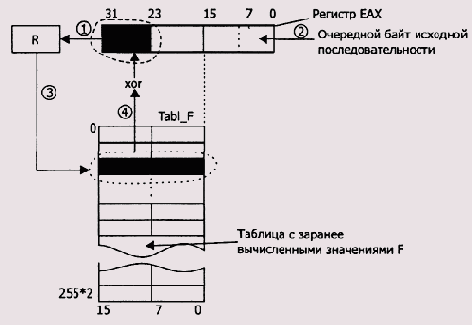
Рисунок 9.8. Общая схема табличного алгоритма

На схеме, показанной на рисунке, цифрами обозначена последовательность шагов табличного алгоритма. Шаги 1 и 2 выполняются одновременно и означают, что старший байт из регистра ЕАХ выдвигается в переменную R, а младший байт этого регистра заполняется очередным байтом исходной последовательности. Значение переменной R используется на шаге 3 в качестве индекса в таблице TABL_F для извлечения 16-битного значения, которое на шаге 4 будет объединено

операцией XOR с содержимым старших 16 битов регистра ЕАХ. Таким образом, в отличие от прямого алгоритма процесс преобразования вырастает до уровня байтов и содержит три операции: сдвига, доступа к таблице для извлечения нужного значения и операции XOR извлеченного значения с содержимым старшей половины ЕАХ. По окончании процесса в старшей половине ЕАХ будет содержаться значение CRC. Сообщение по-прежнему должно быть выровненным, то есть дополненным количеством битов, равным степени полинома, или для данного случая — 16. Для практических приложений это крайне неудобно, и решение этой проблемы будет показано чуть ниже. Пока же разработаем программу вычисления содержимого таблицы на основе полинома 1021h степени 16.

:prg09_03.asm - программа вычисления содержимого таблицы : на основе полинома 1021п степени 16.

.data

tabl_16 dw 256 dup (0) :CRC-таблица

len_tabl_16=$-tabl_16

adr_tabl_16 dd tabl_16

polinom dw 1021h

.code

les di,adr_tabl_16

add di.len_tabl_16-2

std :идем назад по таблице

mov ex.255

mov bx.polinom

ml: xor ax.ax

mov ah.cl :индекс в таблице для вычисления CRC

push ex сложенные циклы

mov ex. 8

m2: shl ax.l

jnc m3 :старшие разряды не равны - выполняем сдвиг

: (частное нас не интересует) ;старшие разряды равны - выполняем XOR:

xor ax.bx :ax XOR polinom

m3: loop m2 _^

pop ex

stosw

loop ml

В результате работы этой программы область памяти tabl_16 будет инициализирована таблицей значений, которые могут быть использованы в схеме вычис-- ления значения CRC исходной последовательности (см. Рисунок 9.8).

Содержание раздела