Прямой алгоритм вычисления CRC

Даже маленькая практика стоит большой теории.
Закон Букера (Прикладная Мерфология)

После всех этих рассуждений мы готовы к тому, чтобы осмысленно воспринять общую схему реального алгоритма вычисления CRC — алгоритма прямого (поразрядного) вычисления CRC. При этом удобно CRC-алгоритм рассматривать с точки зрения двух сторон-участников процесса: источника — объекта, формирующего сообщение для передачи, и приемника — объекта, который принимает сообщение и проверяет его целостность. Действия источника следующие.

1. Выбрать полином Р, в результате автоматически становится известной его степень N.

2. Добавить к исходной двоичной последовательности N нулевых битов. Это добавление делается для гарантированной обработки всех битов исходной последовательности.

3. Выполнить деление дополненной N нулями исходной строки S на полином Р по правилам CRC-арифметики. Запомнить остаток, который и будет являться CRC.

4. Сформировать окончательное сообщение, которое будет состоять из двух частей: собственно сообщения и добавленного в его конец значения CRC.

К примеру, вычисление по этому алгоритму CRC для исходной последовательности 1101001110010110100 (см. Рисунок 9.4) и сама окончательная последовательность на стороне источника будут выглядеть так, как показано на Рисунок 9.5.

Из рисунка видно, что в начале вычисления исходная последовательность 1101001110010110100 дополняется нулями в количестве, равном степени полинома (Р=1011 - степень полинома N=3): 1101001110010110100+000. При выполнении CRC-деления эти дополнительные биты гарантируют, что все биты исходной последовательности примут участие в процессе формирования значения CRC. Результирующая последовательность получается равной исходной последовательности, дополненной значением CRC: 1101001110010110100+011. Заметим, что длина присоединяемого к исходной последовательности значения CRC должна быть равна степени полинома, даже если CRC, как в нашем случае, имеет ведущие нули. Это очень важный момент, понимание которого является ключом к пониманию сути процессов, происходящих на стороне приемника при получении и определении целостности исходного сообщения. Действия алгоритма для приемника просты — выполнить деление полученной последовательности на полином. При этом для выполнения деления нет необходимости дополнять исходную последовательность нулями, тем более что на практике соблюдение этого условия крайне неудобно. Приемник попросту выполняет CRC-деление полученной исходной строки (дополненной в конце

исходным значением CRC) на полином и анализирует остаток. Если остаток от этого деления нулевой, то исходная последовательность не была нарушена во время передачи. В обратном случае существует очень большая вероятность нарушения целостности исходной последовательности, и нужно принимать дополнительные меры по выяснению и исправлению ситуации. Одной из таких мер может быть попытка восстановления нужного значения CRC.

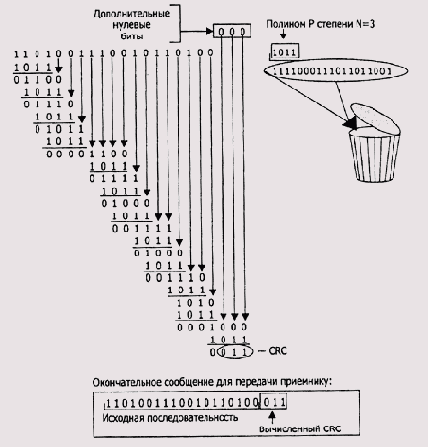
Рисунок 9.5. Схема формирования выходного сообщения из исходного с использованием CRC-алгоритма

Описанный выше алгоритм вычисления значения CRC называется прямым и чаще всего реализуется аппаратно. Но, тем не менее, для совершенствования навыков программирования на ассемблере составим реализующий его пример программы. Хотя эффективность этой программы не слишком высока, у нее есть две учебные цели:

показать в виде программной реализации суть алгоритма вычисления CRC и самого CRC-деления;

подготовить себя к пониманию более совершенных алгоритмов расчета CRC, к которым относится, в частности, рассматриваемый ниже табличный алгоритм.

Для компьютерной реализации алгоритмов вычисления CRC удобно выбирать полиномы со степенями, кратными 8 (то есть размерности регистров) — 8, j5, 24, 32 или даже 64. В этом случае можно подобрать команды из системы команд микропроцессора, наиболее оптимально реализующие алгоритмы вычисления CRC. В качестве полинома выберем один из рекомендуемых полиномов (см. ниже) — 4003. И еще одно важное замечание — степень полинома определяет размерность регистра, используемого в алгоритме, при этом считается, что старший (всегда единичный) бит полинома находится сразу за левой границей регистра. В этих условиях программа реализации прямого алгоритма вычисления CRC функционирует следующим образом (для лучшего понимания в процессе разбора алгоритма см. Рисунок 9.6). В регистр побитно вдвигаются биты исходной строки. Это происходит до тех пор, пока при очередном сдвиге слева появится единичный бит. В этом случае все содержимое регистра подвергается операции XOR со значением полинома без старшего бита. Далее процесс сдвига и анализа выдвигаемого бита продолжается до тех пор, пока не будет выдвинут очередной единичный бит, в результате чего опять между регистром и полиномом выполняется операция XOR, и т. д. После того как последний бит вдвинут в регистр, в него вдвигается количество нулевых битов, равное степени полинома. Этим, как мы не раз уже отмечали, достигается участие всех бит исходной битовой строки в формировании значения CRC. В результате в регистре остается значение CRC, которое необходимо добавить к исходной строке и передать приемнику.

jnc m5 ;старшие разряды не равны - выполняем сдвиг (частное нас не интересует)

;старшие разряды равны - выполняем XOR:

хог eax.ebx;eax(31. .16) XOR pollnom т5: loop m4

В результате вычисления CRC символьной последовательности "6476с8" получим CRC • 35dah.

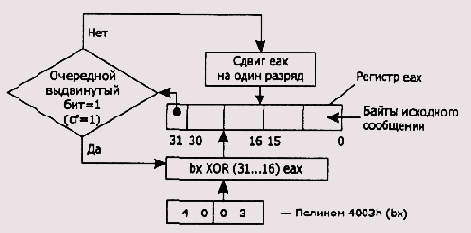
Рисунок 9.6. Схема вычисления значения CRC прямым алгоритмом

Для того чтобы смоделировать действия стороны приемника, можно использовать ту же самую программу со слегка измененными исходными данными — к строке bitstring добавляем вычисленное значение CRC. После этого под отладчиком наблюдаем за процессом CRC-деления, причем контролируем остаток от деления. В определенный момент увидим, что он стал нулевым — это свидетельствует о том, что исходная последовательность не была изменена. Для эксперимента можно изменить значения одного или более битов исходной последовательности и посмотреть, что получится.

;prg09_02.asm - программа демонстрации прямого алгоритма вычисления CRC ;(сторона-приемник).

.data

исходная битовая последовательность в символах

bit_string db "6476c8",35h.0dah

1en_bit_stri ng=$-bi t_stri ng

adr_bit_string dd bit_string

polinomdw 4003h

.code

main:

:см. предыдущую программу

exit: :выход из программы

Очевидный недостаток прямого метода — большое количество операций сдвига, исключающих операций ИЛИ (XOR) и операций условного перехода, которые выполняются для каждого бита исходного сообщения. Поэтому на практике используется другой способ расчета CRC, называемый табличным.

std :идем назад по таблице

mov ex.255

mov bx.polinom

ml: xor ax,ax

mov ah.cl :индекс в таблице для вычисления CRC

push ex сложенные циклы

mov ex.8

m2: shi ax.l

jnc m3 ;старшие разряды не равны - выполняем сдвиг (частное нас не интересует)

:старшие разряды равны - выполняем XOR:

xor ax.bx :ax XOR polinom

тЗ: loop m2

pop ex

stosw

loop ml

-------------закончили расчет CRC-таблицы.........

хог ах,ах

xor bx.bx

Ids si.adrbitstring

mov cx.len_bit_string

m4: mov bl.ah

shl ax.8

xor bl.[si]

xor ax.tabl_16[bx]

inc si

1oop m4

;.........

Рассмотрением этого алгоритма введение в проблему вычисления CRC можно было бы и закончить. Все существующие алгоритмы вычисления CRC являются, по сути, различными модификациями описанного выше табличного алгоритма. Эти модификации преследуют разные цели, перечислим некоторые из них:

переход от цикла по всем битам к циклу по большим порциям данных — байтам, словам и т. д.;

повышение разрядности порождающего полинома;

отражение особенностей функционирования аппаратуры передачи данных (наличие этой цели обусловлено тем, что микросхемы, поддерживающие работу последовательного порта компьютера, передачу байта начинают с его младших битов, поэтому описанные ниже алгоритмы расчета CRC, учитывающие эту особенность, называются зеркальными).

Алгоритмы вычисления CRC получили свое закрепление в некоторых стандартах. Перечислим отличительные особенности основных алгоритмов вычисле-^ ния CRC. Итак, основные алгоритмы вычисления CRC различаются:

по значению и степени порождающего полинома, при этом значение полинома обычно указывается без ведущей единицы в старшем разряде;

по начальному содержимому регистра, в котором формируется значение CRC;

по тому, производится ли обращение битов каждого байта перед его обработкой;

по способу прохода байтов через регистр — способ может быть косвенным или прямым;

по тому, производится ли обращение конечного результата;

по конечному значению, с которым производится объединение по XOR результата вычисления CRC.

После появления 32-разрядных микропроцессоров наибольшей популярностью стали пользоваться 32-разрядные алгоритмы вычисления CRC. В различных источниках рассматривают два типа таких алгоритмов — прямой и зеркальный. Рассмотрим их конкретные реализации, рекомендуемые стандартами.

Содержание раздела