Сборник по задачам и примерам Assembler
     

Необходимость дополнения исходной строки завершающими



Прямой табличный алгоритм CRC16

' Необходимость дополнения исходной строки завершающими нулевыми байтами представляет большое неудобство при реализации общей схемы табличного

алгоритма. Поэтому на практике используют другую схему вычисления CRC, не требующую завершения исходного сообщения нулевыми байтами. В этой схеме

очередной байт исходной строки объединяется операцией XOR со старшим байтом регистра, выдвинутым с левой стороны этого регистра. Полученное в результате объединения значение используется в качестве индекса для доступа к CRC-таб-лице. Извлекаемое из CRC-таблицы значение объединяется операцией XOR с содержимым регистра. Описанный алгоритм называют прямым табличным алгоритмом.



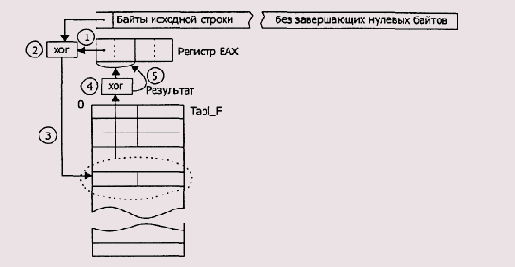
Рисунок 9.9. Схема вычислений CRC с использованием прямого табличного алгоритма

На схеме вычислений CRC с использованием прямого табличного алгоритма цифрами обозначена последовательность шагов вычисления CRC.

  • 1. Выдвижение старшего байта регистра АХ в байтовую ячейку.

    2. Выполнение операции XOR над выдвинутым на шаге 1 в байтовую ячейку старшим байтом регистра АХ и очередным байтом исходной строки.

    3. Полученное на шаге 2 значение используется в качестве индекса для доступа к элементу CRC-таблицы.

    4. Извлеченное из CRC-таблицы значение объединяется по XOR со значением в регистре АХ.

    5. Результат выполнения на шаге 4 операции XOR помещается обратно в регистр АХ.


    • После обработки последнего байта исходной строки регистр АХ содержит значение CRC. Программа вычисления CRC с использованием прямого табличного алгоритма приведена ниже.

    :prg09_04.asm - программа вычисления CRC с использованием прямого табличного алгоритма.



    .......... »

    .data

    ;исходная битовая последовательность в символах

    bit_string db "6476c8"

    1en_bi t_string=$-bi t_stri ng

    adr_bit_string dd bit_string

    tabl_16 dw 256 dup (0) iCRC-таблица

    Ien_tab1_16=$-tabl_16 adr_tabl_16 dd tabl_16

    polinom dw 1021h

    .code

    .-------------расчитываем CRC-таблицу---.....-------------

    les di.adr_tabl_16

    add di.len_tabl_16-2



    std :идем назад по таблице

    mov ex.255

    mov bx.polinom

    ml: xor ax,ax

    mov ah.cl :индекс в таблице для вычисления CRC

    push ex сложенные циклы

    mov ex.8

    m2: shi ax.l

    jnc m3 ;старшие разряды не равны - выполняем сдвиг (частное нас не интересует)

    :старшие разряды равны - выполняем XOR:

    xor ax.bx :ax XOR polinom

    тЗ: loop m2

    pop ex

    stosw

    loop ml

    -------------закончили расчет CRC-таблицы.........

    хог ах,ах

    xor bx.bx

    Ids si.adrbitstring

    mov cx.len_bit_string

    m4: mov bl.ah

    shl ax.8

    xor bl.[si]

    xor ax.tabl_16[bx]

    inc si

    1oop m4

    ;.........

    Рассмотрением этого алгоритма введение в проблему вычисления CRC можно было бы и закончить. Все существующие алгоритмы вычисления CRC являются, по сути, различными модификациями описанного выше табличного алгоритма. Эти модификации преследуют разные цели, перечислим некоторые из них:

  • переход от цикла по всем битам к циклу по большим порциям данных — байтам, словам и т. д.;


  • повышение разрядности порождающего полинома;


  • отражение особенностей функционирования аппаратуры передачи данных (наличие этой цели обусловлено тем, что микросхемы, поддерживающие работу последовательного порта компьютера, передачу байта начинают с его младших битов, поэтому описанные ниже алгоритмы расчета CRC, учитывающие эту особенность, называются зеркальными).


    • Алгоритмы вычисления CRC получили свое закрепление в некоторых стандартах. Перечислим отличительные особенности основных алгоритмов вычисле-^ ния CRC. Итак, основные алгоритмы вычисления CRC различаются:

  • по значению и степени порождающего полинома, при этом значение полинома обычно указывается без ведущей единицы в старшем разряде;


  • по начальному содержимому регистра, в котором формируется значение CRC;

    по тому, производится ли обращение битов каждого байта перед его обработкой;


  • по способу прохода байтов через регистр — способ может быть косвенным или прямым;


  • по тому, производится ли обращение конечного результата;


  • по конечному значению, с которым производится объединение по XOR результата вычисления CRC.


    • После появления 32-разрядных микропроцессоров наибольшей популярностью стали пользоваться 32-разрядные алгоритмы вычисления CRC. В различных источниках рассматривают два типа таких алгоритмов — прямой и зеркальный. Рассмотрим их конкретные реализации, рекомендуемые стандартами.

     

    Содержание раздела